An Introduction to PyTorch & Autograd

Paul O'Grady

#EuroPython, Rimini - 13th July 2017

ME:

Currently a Data Scientist at ...

Twitter: @paul_ogrady

Overview

• Background—Matrix computations & Deep Learning
• PyTorch—Tensors & Variables
• AutoGrad—Gradients & Backpropagation
• Linear regression—Hello world example
• Define-by-run Vs Define-and-run

Background

Matrix computations before Deep Learning/GPUs

• Computation constrained to CPUs
• BLAS: Basic Linear Algebra Subprograms
• LAPACK: Linear Algebra PACKage
• Python: Numpy
• No real Tensor support

Deep Learning

• Deep Learning models contain many millions of model parameters and requires a lot of computational resources
• Tensor (ndarray) operations on the GPU
• Many frameworks have appeared including Theano, Tensorflow, Caffe ...
• Gradients & Automatic/Symbolic differentiation
• Python at the centre of this

PyTorch is the new kid on the block...

PyTorch

PyTorch

• Follows Lua Torch, both use the same underlying C libraries
• PyTorch Beta release was on January 21—v0.1.6
• PyTorch is a define-by-run framework as opposed to define-and-run—leads to dynamic computation graphs, looks more Pythonic
• Main components:
  • torch.nn - Build & train neural networks/models
  • torch.autograd - Automatic differentiation
  • torch.optim - Optimization algorithms

Following examples are for PyTorch Ver 0.1.12 running on Python 3.5.3

PyTorch Status

Deep Learning landscape:

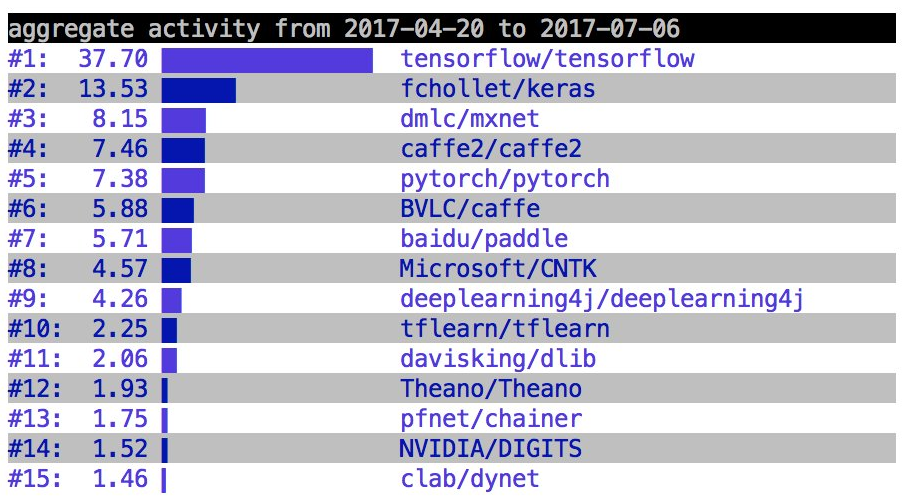
François Chollet (@fchollet)

Tensors

• Tensors are PyTorch's fundamental data abstraction

  >>> import torch
  >>> x = torch.FloatTensor([[1, 2, 3], [4, 5, 6]])
  >>> x
   1  2  3
   4  5  6
  [torch.FloatTensor of size 2x3]
  >>> x.size()
  torch.Size([2, 3])
  

• Supports in-place & out-place operations

  >>> x.add_(torch.ones(2,3) + torch.ones(2,3))
   3  4  5
   6  7  8
  [torch.FloatTensor of size 2x3]
  >>> x.sub_(torch.ones(2,3) * 2)
  

Tensors & Numpy

• Torch plays well with numpy

  >>> import numpy as np
  >>> y_np = np.array([[.5,.5,.5], [.5,.5,.5]], dtype='float32')
  >>> res = x.numpy() * y_np
  >>> res
  array([[ 0.5,  1. ,  1.5],
         [ 2. ,  2.5,  3. ]], dtype=float32)
  >>> type(res)
  <class 'numpy.ndarray'>
  

• Bridge back and forth

  >>> z = np.matrix([[2.,2.], [2.,2.], [2.,2.]], dtype='int16')
  >>> x.short() @ torch.from_numpy(z) # `mm` method
   12  12
   30  30
  [torch.ShortTensor of size 2x2]
  

Tensors

• Reshape tensors using views

  >>> x.view(1,6)
   1  2  3  4  5  6
  [torch.FloatTensor of size 1x6]
  

• Tensor computation can be moved to and from GPU

  >>> if torch.cuda.is_available():
  ...     x = x.cuda()
  ...     y = torch.from_numpy(y_np).cuda()
  ...     x + y
   1.5000  2.5000  3.5000
   4.5000  5.5000  6.5000
  [torch.FloatTensor of size 2x3]
  >>> x.cpu()
   1  2  3
   4  5  6
  [torch.FloatTensor of size 2x3]
  

Variables

• Part of torch.autograd package
• Variable: Thin wrapper around Tensor that allows for
  • Specification of a computation graph
  • Accumulation of gradients
• Variables know what created them Tensors don't
• Variables facilitate backpropagation of gradients & automatic differentiation, requires_grad=True
• At test/inference time Variables are volatile

Variables

• requires_grad allows calculation of gradients w.r.t the variable

  >>> from torch.autograd import Variable
  >>> x = Variable(torch.Tensor([1., 2., 3]), requires_grad=False)
  >>> y = Variable(torch.Tensor([4., 5., 6]), requires_grad=True)
  >>> z = x + y
  >>> z.data.numpy()
  array([ 5.,  7.,  9.], dtype=float32)
  

• Variables keep history...

  >>> z.creator
  <torch.autograd._functions.basic_ops.Add object at 0x7fa1d0294908>
  >>> s = z.sum()
  >>> s
  Variable containing:
   21
  [torch.FloatTensor of size 1]
  >>> s.creator   # grad_fn on master branch
  <torch.autograd._functions.reduce.Sum object at 0x7fa1d0294828>
  

Variable History

• Chase references to construct a computation graph

  >>> def history(var):
  ...     if isinstance(var, Variable):
  ...         print(var.data.numpy())
  ...     else:
  ...         print(str(type(var).__name__))
  ...
  ...     if hasattr(var, 'previous_functions'):
  ...         for func in list(var.previous_functions)[::-1]:
  ...             history(func[0])
  >>> s += 1
  >>> history(s.creator)
  AddConstant
  Sum
  Add
  [ 4.  5.  6.]
  [ 1.  2.  3.]
  >>> s._version
  1
  

AutoGrad

Autograd

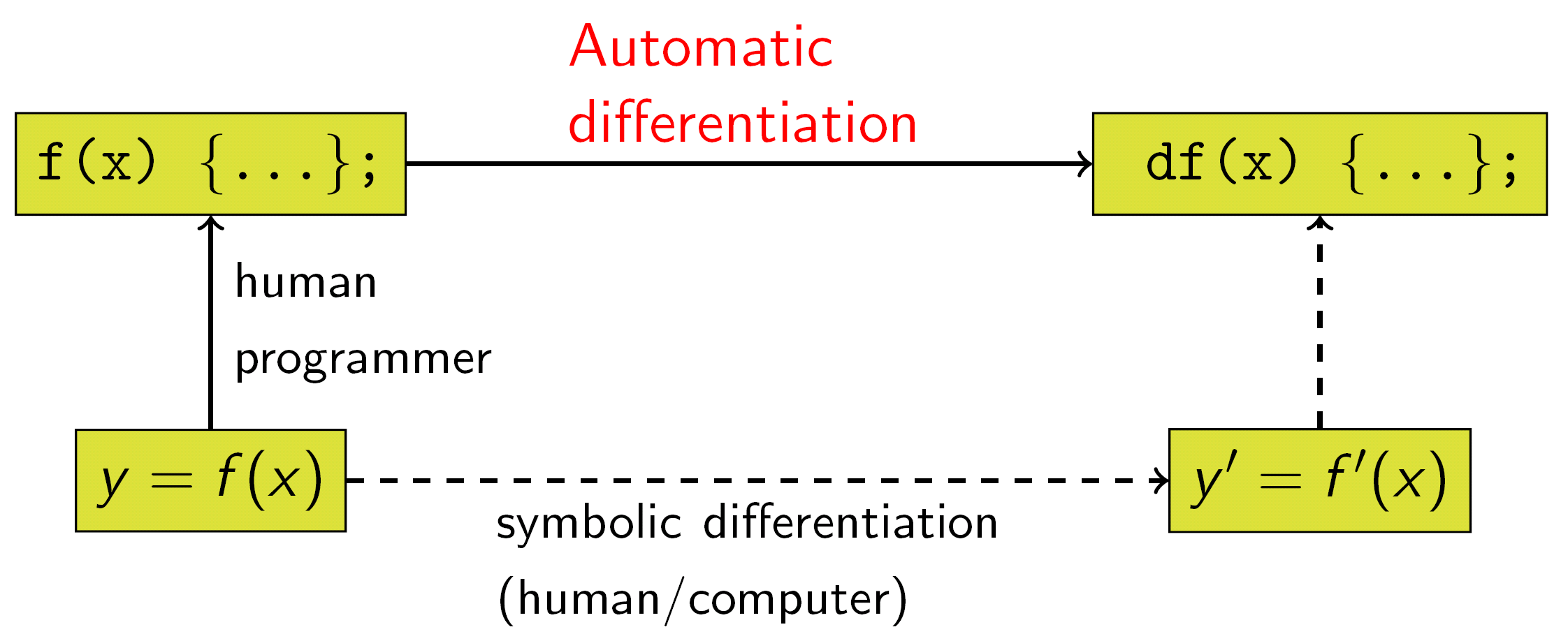
• torch.autograd provides classes and functions implementing automatic differentiation of arbitrary scalar valued functions.
• Reverse-mode auto-differentiation, which allows you to change the way your network behaves arbitrarily with zero lag or overhead.
• Inspired by:
  • Python Autograd
  • Chainer
• "One of the fastest implementations of it to date"
• Requires minimal changes to the existing code—just change Tensors to Variables!

Calculus

Differential Calculus

• Brief reminder:

  \[\frac{dy}{dx} = \lim_{h \to 0}{f(x+h) - f(x)\over{h}}\]
  

• Used to find extrema of functions

Backpropagation

• Used to calculate the gradient of the loss function with respect to the model parameters/layers

• Uses the chain rule to iteratively compute gradients for each layer:

  \[{\frac {dz}{dx}}={\frac {dz}{dy}}\cdot {\frac {dy}{dx}}=f'(y)g'(x)=f'(g(x))g'(x).\]

  where \(z=f(y)\) & \(y=g(x)\).

  e.g. \({\frac {d}{dx}} (3x + 1)^2 = 6(3x + 1)\)

• Autograd implements Backpropagation: torch.autograd.variable.backward

Trig. Differentiation

• Derivative of a function gives gradients

  \[{\frac {d}{dx}} (\sin (x)) = \cos (x)\]

• Example for \(sin(x)\)

  >>> x = Variable(torch.Tensor(np.array([0.,  0.5,  1.,  1.5,  2.])
  ...          * np.pi), requires_grad=True)
  >>> out = torch.sin(x)
  >>> x.grad
  >>> out.backward(torch.Tensor([1., 1., 1., 1., 1.])) # d(out)/dx
  >>> out.data.int().numpy()
  array([ 0,  1,  0, -1,  0], dtype=int32)
  >>> x.grad.data.int().numpy() # Gradients
  array([ 1,  0, -1,  0,  1], dtype=int32)
  >>> torch.cos(x).data.int().numpy()
  array([ 1,  0, -1,  0,  1], dtype=int32)
  

Implementation

• Deep in PyTorch...

  from torch.autograd import Function
  
  class Sin(Function):
  
      @staticmethod
      def forward(ctx, i):
          ctx.save_for_backward(i)
          return i.sin()
  
      @staticmethod
      def backward(ctx, grad_output):
          i, = ctx.saved_variables
          return grad_output * i.cos()
  

• backward contains gradient formula

• Extend PyTorch by creating your own Functions

Quadratic Gradients

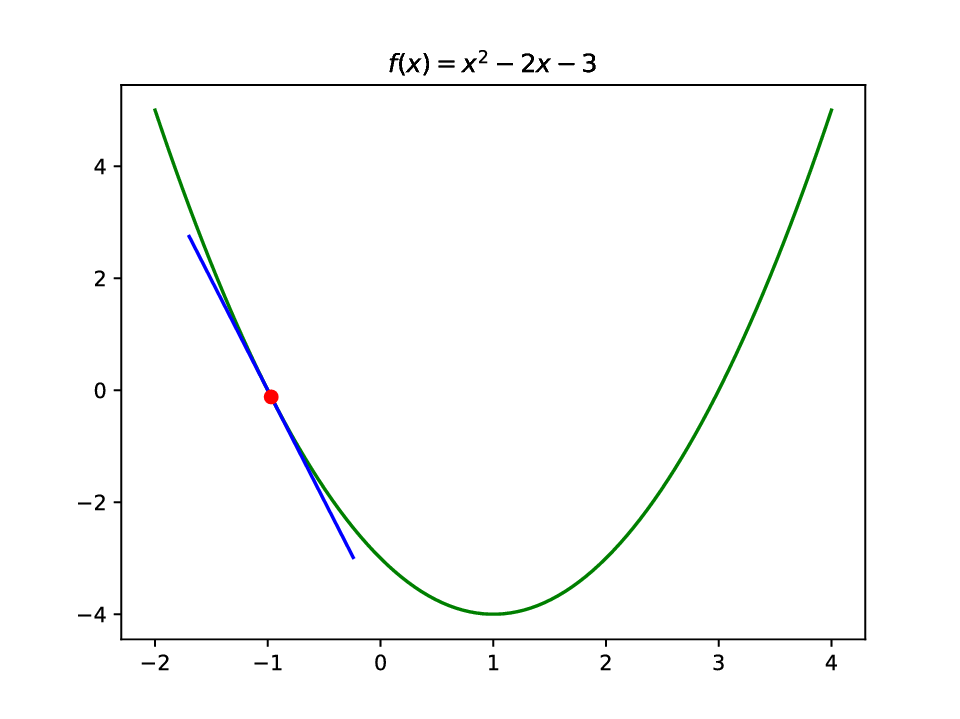
• Quadratic function:

  \[{\frac {d}{dx}} (x^2 - 2x - 3) = 2x - 2\]

• Determine gradient at \(x=-1\)

  >>> x = Variable(torch.Tensor(np.linspace(-2, 4, 100)),
  ...               requires_grad=True)
  >>> y = x**2 - 2*x - 3
  # Calculate the gradient for x=-1
  >>> target = -1
  >>> ind = np.where(x.data.numpy() >= target)[0][0]
  >>> gradients = torch.zeros(100,1)
  >>> gradients[ind] = 1
  >>> y.backward(gradients)
  

Quadratic Gradients

• Determine gradient & tangent line

  >>> x_val = float(x[ind].data.numpy())
  >>> y_val = float(y[ind].data.numpy())
  >>> m = float(x.grad.data.numpy()[ind])
  >>> m
  -3.939393997192383
  
  # Calculate tangent
  >>> y_tangent = m*(x - x_val) + y_val
  >>> x = x.data.numpy()
  >>> y = y.data.numpy()
  >>> y_tangent = y_tangent.data.numpy()
  
  >>> plt.plot(x, y, 'g', x[5:30], y_tangent[5:30], 'b',
  ...          x_val, y_val, 'ro')
  >>> plt.title('$f(x) = x^2 - 2x - 3$')
  >>> plt.show()
  

Tangent

Linear Regression

Linear Regression

• Fit a line to the data: minimize the distance between the points and the line

• Model relationship between \(x\) & \(y\):

  \[y = \alpha x + \beta\]
  • \(\alpha\): weighting
  • \(\beta\): intercept
  • \(x\) Independent variable
  • \(y\) Dependant variable

• PyTorch affine/linear model: torch.nn.Linear

Linear Regression

Machine Learning with Torch

• ML requires: model, cost function & learning alg.

• Mean Square Error: (torch.nn.MSELoss)

  \[\operatorname {MSE}={\frac {1}{n}}\sum _{{i=1}}^{n}({\hat{y_{i}}}-y_{i})^{2}\]

  where \(\hat{y_{i}}\) is the predicted value & \(y_{i}\) is the true value.

• Stochastic Gradient Descent: (torch.optim.SGD)

  \[\theta_{t+1} = \theta_t - \eta \nabla L(\theta)\]

  where \(\theta\) are the model parameters, \(\eta\) is the learning rate & \(\nabla L(\theta)\) is the gradient of the parameters.

Linear Regression

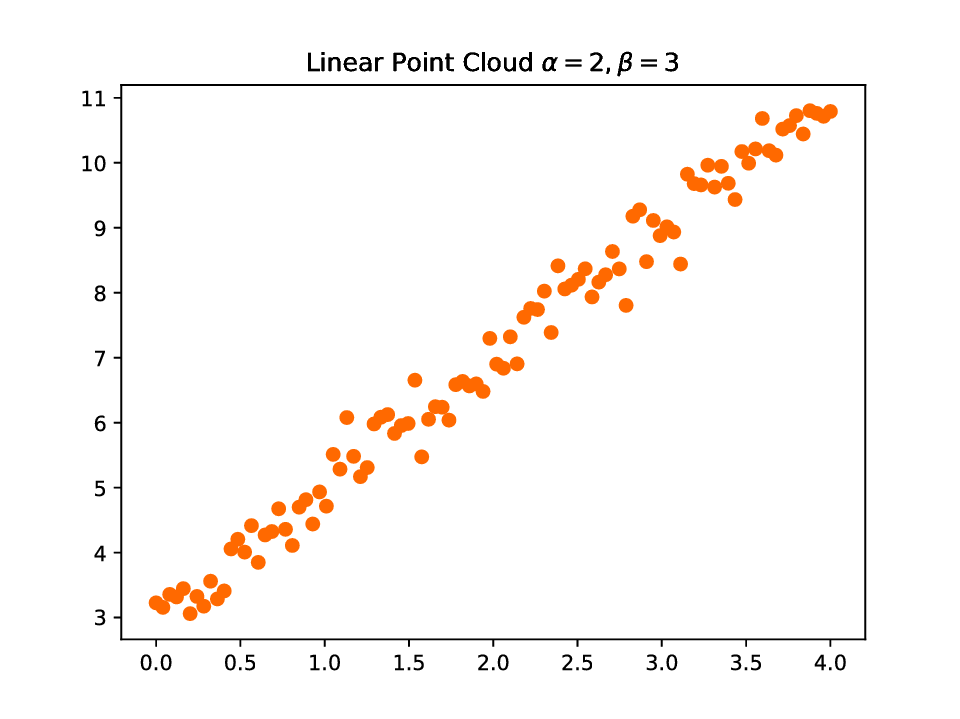
• Create data

  >>> alpha = 2; beta = 3
  >>> x = np.linspace(0, 4, 100)
  >>> y = alpha * x + beta + np.random.randn(100) * 0.3
  >>> x = x.reshape(-1, 1) # convert to column vectors
  >>> y = y.reshape(-1, 1)
  

• Instantiate model

  >>> class LinearRegressionModel(nn.Module):
  ...     def __init__(self, input_dim, output_dim):
  ...         super(LinearRegressionModel, self).__init__()
  ...         self.linear = nn.Linear(input_dim, output_dim)
  ...
  ...     def forward(self, x):
  ...         out = self.linear(x)
  ...         return out
  ...
  >>> model = LinearRegressionModel(input_dim=1, output_dim=1)
  

Linear Regression

• Instantiate criterion & optimizer. Prepare training data

  >>> criterion = nn.MSELoss()
  >>> optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
  
  >>> inputs = Variable(torch.from_numpy(x.astype('float32')))
  >>> labels = Variable(torch.from_numpy(y.astype('float32')))
  

• Inspect model parameters

  >>> list(model.named_parameters())
  [('linear.weight', Parameter containing:
   2.3494
  [torch.FloatTensor of size 1x1]
  ), ('linear.bias', Parameter containing:
   2.1157
  [torch.FloatTensor of size 1]
  )]
  

Linear Regression

• Train model over 250 epochs

  >>> for epoch in range(250):
  ...     # 1. Clear gradients w.r.t. parameters
  ...     optimizer.zero_grad()
  ...
  ...     # 2. Forward to get output
  ...     outputs = model(inputs)
  ...
  ...     # 3. Calculate Loss (Scalar value)
  ...     loss = criterion(outputs, labels)
  ...
  ...     # 4. Calculate gradients w.r.t. parameters
  ...     loss.backward()
  ...
  ...     # 5. Updating parameters
  ...     optimizer.step()
  

Define-By-Run

Linear Regression

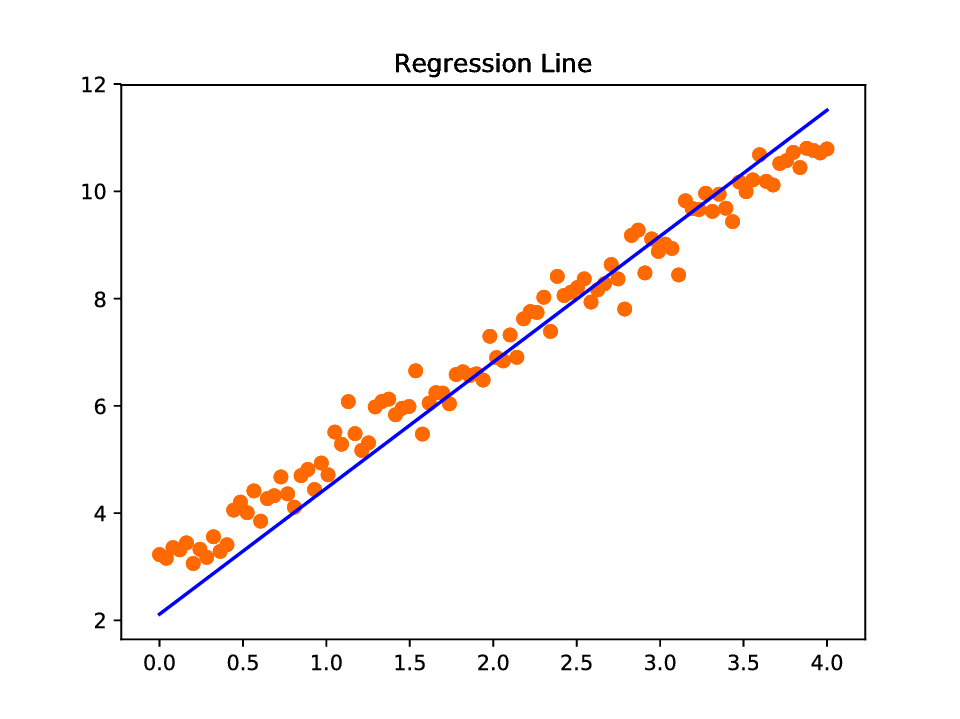
• Inspect learned parameters

  >>> list(model.named_parameters())
  [('linear.weight', Parameter containing:
   2.3221
  [torch.FloatTensor of size 1x1]
  ), ('linear.bias', Parameter containing:
   2.1034
  [torch.FloatTensor of size 1]
  )]
  

• Inspect network modules/layers

  >>> for idx, m in enumerate(model.named_modules()):
  ...     print(idx, '->', m)
  ...
  0 -> ('', LinearRegressionModel (
    (linear): Linear (1 -> 1)
  ))
  1 -> ('linear', Linear (1 -> 1))
  

Linear Regression

Theano - Define-And-Run

• Contrast with Theano; Model setup

  >>> import theano
  >>> from theano import tensor as T
  >>> import numpy as np
  
  >>> # Generate training data
  >>> trX = np.linspace(-1, 1, 101)
  >>> trY = 2 * trX + np.random.randn(*trX.shape) * 0.33
  
  >>> # Symbolic variable initialization
  >>> X = T.scalar()
  >>> Y = T.scalar()
  
  >>> # Define model
  >>> def model(X, w):
  ...     return X * w
  >>> # Model parameter initialization
  ... w = theano.shared(np.asarray(0., dtype=theano.config.floatX))
  >>> y = model(X, w)
  

Theano - Define-And-Run

• Model training

  >>> # Define cost function, gradient and update rule
  >>> cost = T.mean(T.sqr(y - Y))
  >>> gradient = T.grad(cost=cost, wrt=w)
  >>> updates = [[w, w - gradient * 0.01]]
  
  >>> # Compile to a Python function
  >>> train = theano.function(inputs=[X, Y], outputs=cost,
  ...                 updates=updates, allow_input_downcast=True)
  
  >>> # Run for 100 iterations
  ... for i in range(100):
  ...     for x, y in zip(trX, trY):
  ...         train(x, y)
  

No opportunity to change things within Loop

Summary

• Introduced PyTorch using simple matrix computations & demonstrated Numpy bridge
• Demonstrated dynamic computation graphs using Variables
• Discussed Autograd & Gradients
• Presented a simple linear regression example
• Illustrated Define-by-run Vs define-and-run

Questions?

References